
CRPC Researchers Solve Traveling Salesman Problem for Record-Breaking 13,509 Cities
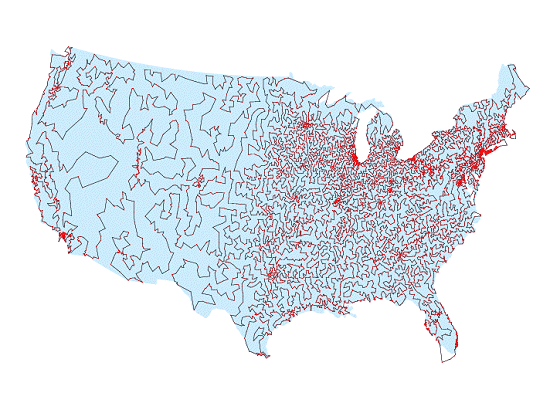 13,509 U.S. cities with populations of more than 500 people connected optimally using methods developed by CRPC researchers. 13,509 U.S. cities with populations of more than 500 people connected optimally using methods developed by CRPC researchers. |
CRPC Researchers David Applegate, Robert Bixby, and William Cook (Rice University) and Vasek Chvatal (Rutgers University) have determined a breakthrough solution to the Traveling Salesman Problem (TSP), a method for finding an optimal path for a salesman to take when traveling through a specified number of cities. The researchers have solved the TSP for 13,509 U.S. cities with populations of more than 500 people, a dramatic step beyond their previous record of 7,397 cities, set in 1994.
The TSP is typical of a class of hard optimization problems with applications in science and engineering that has intrigued mathematicians and computer scientists for years. Finding an optimal route for the TSP becomes more challenging as the number of cities increases. For example, to solve for the most economical way a salesman can tour five cities, a computer can be used to calculate the lengths of all 120 possible different routes and find the shortest one in a fraction of a second. However, using the same method to figure the optimal route for 100 cities could take billions of years. The research team has been developing mathematical models and using high-performance computing since 1988 to develop a more efficient solution.
The researchers' first breakthrough was a record 3,038 cities set in 1992, using 50 workstations and an algorithm they designed based on a technique called "cutting planes." The technique steadily improves the collection of linear inequalities describing the set of feasible solutions. This achievement was recognized by Discover magazine as one of its top 50 science stories that year. By 1993, the team had solved for 4,461 cities. This year, the TSP researchers surpassed their 1994 record by using a cluster of three Digital AlphaServer 4100s (a total of 12 processors) and a cluster of 32 Pentium-II PCs located in Rice University's Duncan Hall. The calculation took approximately three months from start to finish.
"The solution of usa13509 is certainly the high point of our research project," says Cook, Noah Harding Professor of Computational and Applied Mathematics (CAAM) at Rice. "Over the past 4 years, we have written an entirely new system for solving the TSP, focusing on methods that can scale up to instances having 10,000 or more cities. The breakthrough in our work came early last year when our team devised a technique for greatly extending the use of linear programming methods for the TSP."
"One the most exciting aspects of this work was the fact that it was truly interdisciplinary," says Bixby, Professor of CAAM. "It involves ideas from polyhedral combinatorics and combinatorial optimization, integer and linear programming, computer science data structures and algorithms, parallel computing, software engineering, numerical analysis, graph theory, and more."
Direct applications of the TSP range from drilling holes in printed circuit boards to designing fiber-optic communications networks, and from routing helicopters around oil rigs to picking up coins from telephone booths. The real mission of this work, however, is the study of techniques that can be used to solve a more general class of applied problems known as mixed-integer programming (MIP) problems. Bixby has created the world's leading software for MIP.
"One of the basic computational tools used in the standard approaches to the TSP, including ours, is linear programming [LP]," says Bixby. "Indeed, the TSP is one of the more demanding uses of this tool, and over the last 10 years has led to numerous advances in the commercial LP software that we were using. These advances then became available to commercial and research users throughout the world. Specially for MIP, we developed a new 'branching rule' called 'strong branching,' which is particularly useful in the solution of difficult integer programs. This branching rule is now available in several commercial MIP solvers."
Of the team's ongoing, breakthrough TSP research, Rutgers Computer Science Professor Chvatal says, "It's addictive. No matter how much progress you make, you always have the nagging feeling that you still did not nail down a couple of hunches that could bring about another quantum leap. And even if we stopped today, cold turkey, the sheer volume of what we have already done is overwhelming. If we printed our code, it would run to well over a thousand pages."
The TSP project is supported by Rice University; the CRPC; Digital Equipment Corporation; and the Keck Foundation, as part of the W.M. Keck Center for Computational Discrete Optimization.
Sites &
Affiliations | Leadership | Research & Applications | Major
Accomplishments | FAQ | Search | Knowledge &
Technology Transfer | Calendar of
Events | Education
& Outreach | Media
Resources | Technical Reports &
Publications | Parallel Computing Research Quarterly Newsletter | News Archives | Contact
Information
Hipersoft | CRPC