
Spring/Summer 1999
Volume 6, Issue 2
Spring/Summer 1998
Volume
3, Issue 1
January 1995
Volume
2, Issue 4
October 1994
Volume
2, Issue 1
January 1994
Research Focus
SURFACE FLOW MODELING OF BAYS, ESTUARIES, AND COASTAL OCEANS
Mary F. Wheeler, Clint N. Dawson, Srinivas Chippada, H. Carter Edwards, The University of Texas; Monica L. Martinez, Rice University
In recent years, there has been considerable interest in the numerical solution of shallow water flow equations. The applications of these equations are numerous, and include modeling tidal fluctuations, for organizations interested in capturing tidal energy for commercial purposes; predicting tidal ranges and surges, which can then be used in the development planning of coastal areas; and, upon coupling to a transport model, considering flow and transport phenomenon. The latter application makes it possible to study remediation options for polluted bays and estuaries, to predict the impact of commercial projects on fisheries, to model salinity intrusion effects, and to study the effects of wetting-induced mineral seepage into streams.
Currently, there exist various hydrodynamic models based on differing philosophies-from those based on the primitive formulation to those based on the wave formulation and from those using finite-difference to those using finite-element or finite-volume methods. Questions on correct physics, numerical stability, numerical convergence, physical time-scale, and numerical time-stepping still persist.
Under the direction of Mary F. Wheeler, the Center for Subsurface Modeling (CSM) at the University of Texas at Austin and collaborators at the University of Houston, the University of Notre Dame, the Waterways Experiment Station, and the Texas Water Development Board have taken efforts in the past two years to answer some of these mathematical questions. They are also pursuing relevant parallel computational issues such as domain decomposition and load balancing.
At the onset of this partially NSF-funded initiative, the CSM began experimentation with a state-of-the-art hydrodynamic flow simulator based on a Galerkin finite element method for solving the wave formulation of the shallow water equations. The CSM was able to develop stability and error estimate analysis for the full non-linear wave formulation and thus contribute to the current literature, which until now has only included analysis for the linearized equations.
Simultaneously, the CSM has developed finite-volume Godunov methods, based on the primitive formulation, that appear competitive with the shallow water flow simulator. An advantage to the former model is its shock-capturing ability that improves resolution along coastal and island boundaries.
Moreover, in recent months the CSM has made tremendous strides in the parallelization of the shallow water flow simulator. The parallelization uses a general message passing library developed by the CSM that runs under Message Passing Interface (MPI), Portable Instrumented Communication Library (PICL), and Parallel Virtual Machine (PVM). No global arrays are used. A preprocessor and a postprocessor were written to handle data decomposition as well as input and output.
The CSM has recently begun using a Hilbert space-filling curve (HSFC) decomposition strategy that enforces nearest neighbor groupings which, in conjunction with load balancing, reduces the amount of processor communication compared to a naive decomposition approach in which nearest neighbor groupings are not explicitly enforced.
CSM researchers conducted a speed-up study on the Intel Paragon over 2, 4, 8, 16, and 32 processors, measured relative to 2 processors, using a 10,147-node, 18,578-element computational domain corresponding to the Gulf of Mexico and the western Atlantic Ocean along the U.S. East Coast (Figure 1). The theoretical speed-up rates were 1, 2, 4, 8, and 16. The naive decomposition strategy yielded speed-up rates of 1.00, 1.85, 3.36, 5.37, and 7.57; however, the HSFC decomposition strategy yielded rates of 1.00, 1.98, 3.85, 6.28, and 10.41.
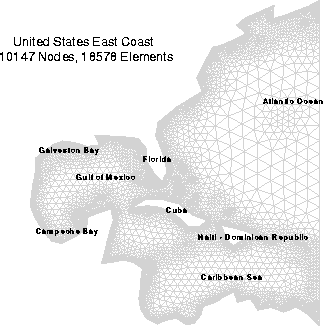
Example of a Computational Domain
For example, in the 4-processor case, the SV ranged from 6.0 to 9.3% for the naive approach compared to ratios ranging from 1.0 to 3.2% for the HSFC approach. Figure 2 shows the naive decomposition on the above computational domain partitioning it into 4 subdomains, and Figure 3 shows the HSFC decomposition.
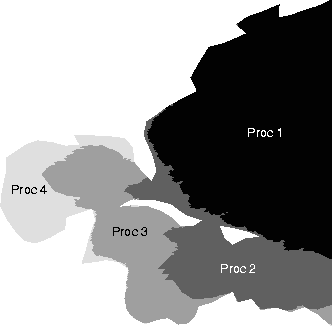
Naive Decomposition Over 4 Processors
Figure 3
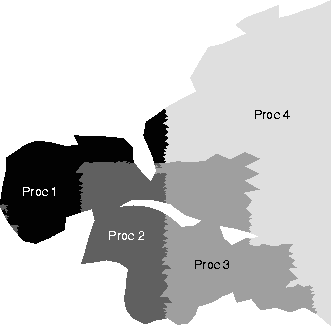
HSFC Decomposition Over 4 Processors
For more information on this project and on other CSM-related projects, see http://www.ticam.utexas.edu/Groups/SubSurfMod/home.html . For an historical and mathematical explanation of space-filling curves, refer to Hans Sagan, Space-Filling Curves, Springer-Verlag, New York, 1994.