
Spring/Summer 1999
Volume 6, Issue 2
Spring/Summer 1998
Volume
3, Issue 1
January 1995
Volume
2, Issue 4
October 1994
Volume
2, Issue 1
January 1994
Global Optimization Techniques with Application to the Least Squares Phase Problem in X-Ray Crystallography
G.N. Phillips Jr., Department of Biochemistry and Cell Biology; and R.A. Tapia, L. Velázquez, and Y. Zhang, Computational and Applied Mathematics, Rice University
Since the beginning of this century, different techniques have been employed to determine the molecular structure of proteins to facilitate scientists' understanding of the compositions of these molecules and their relevant functions in the human body. Scientists perform an X-ray crystallography experiment in which a beam of X-rays is passed through a crystallized protein, and diffracted X-rays emerge from the crystal at different angles and intensities. These intensities are recorded on detection film; however, the phase information cannot be obtained from the experiment. The diffracted pattern gives partial information about the atomic positions in a crystal, and the 3-dimensional structure of the crystallized protein cannot be determined without further computation. This is what is known as the phase problem in X-ray crystallography.
The phase problem can be posed as a global optimization nonlinear least squares (NLS) problem whose objective function represents the error between the intensity measurements and the calculated intensities of the nonlinear model that must be driven to a small value. The objective function is highly nonlinear and nonconvex, which implies the existence of many local minima and makes it difficult to locate the desired global minimizer.
Currently, laborious and time-consuming laboratory techniques are used to construct reasonably accurate macromolecular structures before computational techniques are applied at the final stage of local refinement. Researchers from the Department of Biochemistry and Cell Biology and the Computational and Applied Mathematics Department at Rice University are addressing the semi-local refinement stage of the phase problem, where the objective is to obtain atomic parameters that are more precise than those obtained from an initial structure provided by the scientists. Even by taking advantage of this information, it is still a challenging problem that requires the application of global and local techniques.
The researchers are investigating techniques for solving problems in which the level of the minimal residual error and a "good" initial structure is available. They are proposing two techniques for such problems: a modified Newton's method and a weighting scheme. These techniques can not only be applied to the phase problem where a zero or small residual in the objective function is desired, but also to other application areas, like seismic problems, that can also be modeled as least-squares problems. The objective is to provide better semi-local optimization techniques to obtain an atomic arrangement that fits the experimental intensity data better than those obtained from an initial structure. A related objective is to surpass the benchmark of currently available methods for solving this stage of the phase problem.
Formulation of the NLS Problem
This is a minimization problem in which the objective function f(x) is a sum-of-squares
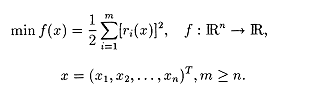
NLS problems often arise in data-fitting applications. In the following example, data (ti,yi) needs to fit in a nonlinear model
The variable x needs to be chosen so that
The residual of the discrepancies is denoted by
General Case
Generally, M models a biological or physical system, x is a collection of parameters in the model, and f(x) measures the discrepancy between predicted and observed values. We want to choose x so that the predicted/calculated values of M(x,ti) agree reasonably well with the observed values of the given system.
X-ray Crystallography
The NLS problem that arises in an X-ray crystallography experiment consists of unknown parameters that represent the positions of atoms within a given molecule and observations that are the intensity data gathered from an experiment.
Formulation of the Phase Problem
The following section contains the mathematical model of the phase problem and an overall discussion of the numerical experimentation conducted using the modified Newton's method technique and the weighted scheme that attempt to solve the semi-local stage of the phase problem. A detailed discussion of how these proposed techniques are actually being implemented to solve small phase problems will be available in a future technical report. Let pm = (hm,km,lm), rj = (xj,yj,zj), r = (r1,r2,...,rn)T where m = 1,...,M and j = 1,...,n. The scattering function can be represented as a complex valued function
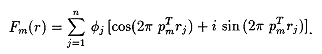
Given experimental intensities Im, locate the atomic positions r as the global solution of the unconstrained minimization problem
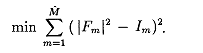
Initial Progress
Researchers have gained a solid understanding on the mathematical model of the problem and the problem itself. Some encouraging results have been obtained. Using an averaging principle, they have derived a set of weights for use in a weighted least squares formulation that makes the resulting objective function smoother with less local minima. The numerical experimentation that the researchers have been conducting deals with phase problems of small molecules (up to 22 atoms). The semi-local and global stages of small problems have been successfully solved, but it gets more complicated as larger problems are attacked. The group will continue attacking the problem for larger molecules. One of the immediate goals is to be able to come up with a better method for solving the semi-local phase problem, which begins with a reasonable starting guess of the positions of the atoms. It is still a challenging problem, and techniques are being developed to improve over the available software in the field. The researchers are currently focused on solving a prototype molecule that consists of 39 atoms. They are adding some extra information into the model in order to obtain the correct configuration with more acceptable accuracy when compared to other techniques.

Figure 1: Molecule of 22 atoms (66 variables)

Figure 2: Molecule of 39 atoms (117 variables)
Future Work
Global optimization problems are extremely difficult. A class of modified Newton methods and properly chosen weighting schemes can be useful tools for least squares global-minimization. Our preliminary numerical experience demonstrates that a combination of the two is sufficient for solving some small problems. It remains to be seen how these techniques can be used as building blocks to construct more powerful algorithms to attack large-scale problems. The current research involves implementing the proposed techniques for a more realistic model, i.e., by adding temperature-factor and scattering-factor information to the model. The problem is being solved first as an unconstrained problem, but later it will be formulated as a constrained nonlinear least-squares minimization problem which can be solved by interior-point techniques.
The researchers are working to provide better semi-local performance than Shelx-97 software packgage (G. Sheldrick), a state-of-the-art Fortran program. This software package will serve as a benchmark for measuring improvements. They plan to combine other global optimization methods (e.g. global continuation) and other weighting schemes to the phase problem.
This work was presented in a poster session by L. Velazquez at the W.M.
Keck Center Annual Research Conference (see "New Research in Computational
Biology Discussed at Keck Conference," this issue). For more
information on
this work, see http://www.caam.rice.edu/~leti.