
A groundwater flow or transport problem requires the solution of a second order elliptic equation with a tensor hydraulic conductivity or dispersion. These problems are posed over an aquifer domain with varying topography due to the geological layering, surface features, and the like.
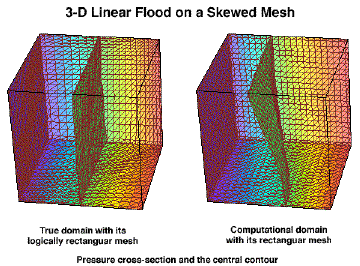
To efficiently handle these difficulties, we developed a cell-centered finite difference method with a stencil of 9 points in 2-D and 19 points in 3-D. The method uses a logically rectangular, curved grid, obtained from a map between the true aquifer domain and a rectangular, computational grid. The method conserves mass locally, and it is highly accurate.
We show a simple test case of a linear pressure drop across a domain with a curved grid. We also show the same solution on teh computational domain.