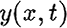From Hansen and Spies [1] we extract a model for a two-layer beam in which slip can occur along the interface. We assume that an adhesive layer of negligible thickness and mass bonds the two adjoining surfaces in such a way that the restoring force created by the adhesive is proportional to the amount of slip. In particular, the transverse displacement, , and the slip, 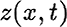, satisfy

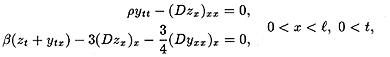
where 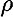, , 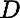and 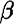denote density, flexural rigidity, and adhesive damping. If each layer is a one meter length of steel that is 0.005 meters thick then 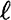= 1, 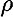= 2000, and 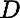= 56250 are suitable choices. In addition we shall suppose the beam to be pinned at its ends, i.e.,

and

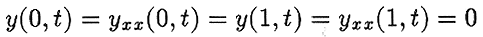
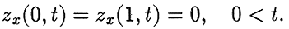
This leaves the choice of 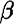to the designer. We propose that 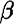be distributed in such a way that the rate of decay of energy is minimized. This decay rate, 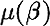, corresponds to the spectral abscissa of the matrix differential operator obtained by writing the first equation as a first order system. In particular,

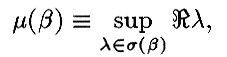
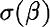where is the spectrum of

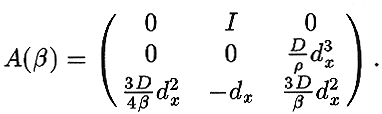
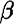If is a positive function then the spectrum of 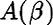will lie in the left halfplane and so 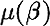will be negative. The design objective is to make it as negative as possible. More precisely, we address

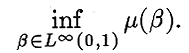
Though 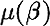may appear as an obvious choice of objective function one rarely finds it in the literature, perhaps for the reason that it suffers doubly, being neither Lipschitz, nor easy to estimate. We address these obstacles in the next section.