The figure below illustrates how the use of a high-order Godunov method can resolve shock formations.

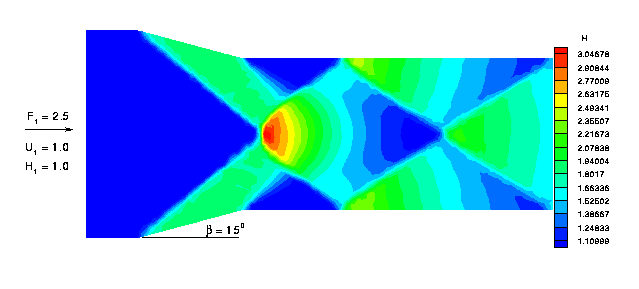
The figure shows a complex series of shocks and rarefactions that are partially the result of the variable cross-section of the domain.

The domain shown consists of an inlet at the left and an outlet at the right. One can visualize this domain, looking down from some fictitious helicopter, as a channel with a variable constriction. The observer wonders what happens as fluid enters from the left, moving right, past the angled section, and into the narrower region.

As the fluid enters the narrower portion of the channel and hits the angled section, the fluid along the walls, now with increased pressure, moves at an angle towards the center of the channel. The wave fronts coming off the angled walls of the channel and the wave fronts coming from the center of the inlet collide at the center of the channel.

A shock forms when the wave travels from, say, a high pressure region to a low pressure region. At the time the wave reaches the low pressure region, the fluid density and pressure in that region jumps to higher values (and all of the state variables are discontinuous).

It is these jumps in pressure that one observes in the `X' designs. For instance, at the vertex of the leftmost `X', one observes the fluid pressure value become higher (red) as the waves off the angled walls (green) collide with waves coming from the center of the inlet (dark blue).

Also notice the rarefaction of the waves that follows the shock. This rarefaction is seen as the smooth degradation of color from red to dark blue in the diamond shape region between the two X's.

In the context of shallow water equations, we can solve for fluid depth instead of pressure via a state equation giving a relation for these two variables. Thus, in this figure, pressure really corresponds to water depth.

Methodology: High-order Godunov method based on the primitive formulation of shallow water equations -- at steady state.

Applications: Flow in variable-width channels and rivers.