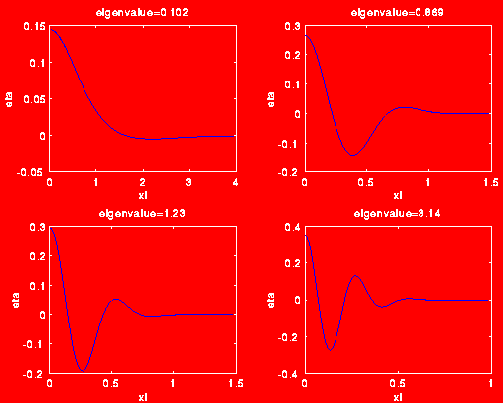
The eigenvalue problem couples the interface and the temperature field, and
is solved on an infinite domain. The computed eigenvalue corresponds to the
growth rate of the crystal, and the computed eigenvector consists of both the
the interface and temperature perturbation. Using a straightforward
transformation, we map the parabolic interface of the stationary solution
to a horizontal line in an infinite rectangular domain. It is observed from
the following picture that the interface becomes more oscillatory as the
growth rate increases, which confirms the Mullins-Sekerka instability theory.