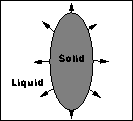
Image that a piece of crystal is placed in some undercooled liquid.
As the crystal freezes, the interface between the solid and the liquid
starts to change. The solid phase grows rapidly from the crystal by sending
out branching fingers. This phenomenon is also called dendritic
solidification, and is responsible for the complicated interface
observed in snowflakes.
Numerical simulations and modeling of crystal growth and dentridic solidification are difficult to obtain because of the moving boundary. We are interested in analyzing the stability of a well known stationary solution that corresponds to a simple parabolic shaped moving front. The standard techniques of linear stability analysis lead to an eigenvalue problem. In particular, the rightmost eigenvalues of some convection diffusion operator are of interest. The stationary solution is said to be stable if there is no eigenvalue of positive real part.
The particular software package we used in our computation is ARPACK, a package that implements the Implicitly Restarted Arnoldi Iteration . We are able to obtain the desired eigenvalues and eigenvectors of the matrix of order 10,000 or larger in a reasonable amount of time.